Skalare und Vektorgrößen waren unter Physikern viele Jahre lang ein heftiges Diskussionsthema. Es bedurfte vieler Studien und Veröffentlichungen, bis sich ein deutlicher Unterschied zwischen den beiden Größen herausstellte. Heutzutage ist es recht einfach, zwischen einer Skalar- und einer Vektorgröße zu unterscheiden.
Contents
Skalare Menge
Die skalare Größe wird durch nur ein Element definiert, das als Betrag bezeichnet wird , ohne das es keine skalare Größe gibt. Daher wird ein Skalar normalerweise als physikalische Größe bezeichnet, die nur eine Größe und keine anderen Eigenschaften hat. Magnitude bedeutet die Größe der Größe wie Länge oder Stärke.
Ein Skalar ist eine beliebige Zahl, die die Größe oder Größe einer Größe angibt, daher muss eine Maßeinheit wie Grad oder Meter an die Zahl angehängt werden. Jede Zufallszahl ist kein Skalar. Zum Beispiel ist Nummer 25 bedeutungslos, es sei denn, Sie sagen uns, dass 25 ein Maß für etwas wie Entfernung, Zeit oder Temperatur ist.
Was Sie über skalare Menge wissen müssen
- Skalare Größe impliziert, dass die physikalische Größe nur eine Größe und keine Richtung hat.
- Jede Änderung der skalaren Größe zeigt nur eine Änderung der Größe der betreffenden physikalischen Größe an.
- Skalare Größen sind immer eindimensional.
- Die Skalargröße kann eine andere Skalargröße teilen.
- Die skalare Größe folgt den gewöhnlichen Regeln der Algebra. Daher kann die normale algebraische Methode verwendet werden, um skalare Größen zu lösen.
- Jede mathematische Berechnung/Operation zwischen zwei oder mehr Skalargrößen führt immer zu einer Skalargröße.
- Jede mathematische Operation zwischen einer Skalargröße und einer Vektorgröße führt immer zu einer Vektorgröße.
- Skalare Menge kann nicht aufgelöst werden; es hat in allen Richtungen genau den gleichen Wert.
Beispiele für skalare Größen
- Geschwindigkeit
- Arbeit
- Distanz
- Leistung
- Temperatur
- Volumen
- Aufladen
- Gravitationspotential
- Frequenz
- Energie
- Länge
- Kinetische Energie
- Spezifische Wärme
- Leistung
- Kalorie
- Dichte
- Entropie
Anzahl der Vektoren
Eine Vektorgröße kann durch zwei Elemente definiert werden, Betrag und Richtung. Ohne diese beiden Elemente kann eine physikalische Größe nicht als Vektor definiert werden. Daher kann eine Vektorgröße als physikalische Größe definiert werden, die sowohl eine Größe als auch eine Richtung umfasst. Magnitude bedeutet die Größe der Größe wie Länge oder Stärke. Richtung bedeutet die Position, auf die der Vektor zeigt oder wohin er gerichtet ist, z. B. nach links oder rechts, Osten, Westen, Norden oder Süden (nach oben oder unten).
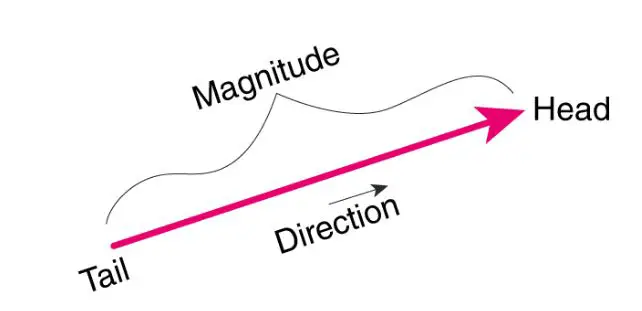
Wenn ein Vektor gezeichnet wird, wird er durch einen Pfeil dargestellt, dessen Länge die Größe des Vektors darstellt und dessen Pfeilspitze in die Richtung des Vektors zeigt.
Was Sie über Vektorquantität wissen müssen
- Vektorgröße impliziert, dass die physikalische Größe sowohl Größe als auch Richtung umfasst.
- Jede Änderung der Vektorgröße zeigt Änderungen entweder in der Größe oder in der Richtung oder in beiden an.
- Vektorgrößen können entweder ein-, zwei- oder dreidimensional sein.
- Zwei Vektoren können nicht oder nie geteilt werden.
- Vektorregeln folgen den Regeln jeder mathematischen Operation. Die Geometriemethode kann verwendet werden, um die Vektorgröße zu lösen.
- Eine mathematische Operation zwischen zwei oder mehr Vektorgrößen kann entweder eine Vektor- oder eine Skalargröße ergeben.
- Eine mathematische Operation zwischen Vektor- und Skalargrößen führt zu einer Vektorgröße.
- Die Vektorgröße kann in zwei zueinander senkrechten Richtungen unter Verwendung des benachbarten Winkels aufgelöst werden.
Beispiele für Vektorgrößen
- Macht
- Beschleunigung
- Last
- Scherspannung
- Geschwindigkeit
- Elektrische Feldstärke
- Zentrifugalkraft
- Drehmoment
- Schwung
- Elektrischer Fluss
Größen, die sowohl vektoriell als auch skalar sind
- Masse
- Gewicht
- Geschwindigkeit
- Arbeit
- Leistung
- Energie
- Verschiebung
- Distanz
- Macht
- Drehmoment
Lesen Sie auch: Unterschied zwischen Masse und Gewicht
Unterschied zwischen Skalar- und Vektorgröße in Tabellenform
| VERGLEICHSGRUNDLAGE | SKALARMENGE | ANZAHL DER VEKTOREN |
| Beschreibung | Skalare Größe impliziert, dass die physikalische Größe nur eine Größe und keine Richtung hat. | Vektorgröße impliziert, dass die physikalische Größe sowohl Größe als auch Richtung umfasst. |
| Ändern | Jede Änderung der skalaren Größe zeigt nur eine Änderung der Größe der betreffenden physikalischen Größe an. | Jede Änderung der Vektorgröße zeigt Änderungen entweder in der Größe oder in der Richtung oder in beiden an. |
| Dimensional | Skalare Größen sind immer eindimensional. | Vektorgrößen können entweder ein-, zwei- oder dreidimensional sein. |
| Aufteilung der Menge | Die Skalargröße kann eine andere Skalargröße teilen. | Zwei Vektoren können nicht oder nie geteilt werden. |
| Mathematische Regeln | Die skalare Größe folgt den gewöhnlichen Regeln der Algebra. | Vektorregeln folgen den Regeln jeder mathematischen Operation. |
| Mathematische Operation zwischen zwei oder mehr Größen | Jede mathematische Berechnung/Operation zwischen zwei oder mehr Skalargrößen führt immer zu einer Skalargröße. | Eine mathematische Operation zwischen zwei oder mehr Vektorgrößen kann entweder eine Vektor- oder eine Skalargröße ergeben. |
| Mathematische Operation zwischen einer Skalargröße und einer Vektorgröße | Jede mathematische Operation zwischen einer Skalargröße und einer Vektorgröße führt immer zu einer Vektorgröße. | Eine mathematische Operation zwischen Vektor- und Skalargrößen führt zu einer Vektorgröße. |
| Richtung | Kann nicht gelöst werden; es hat in allen Richtungen genau den gleichen Wert. | Kann in zwei zueinander senkrechten Richtungen unter Verwendung des benachbarten Winkels aufgelöst werden. |
Was sind einige der Ähnlichkeiten zwischen der skalaren Menge und der Vektormenge?
- Beide haben eine bestimmte Einheit und Dimension.
- Sowohl Skalar als auch Vektor haben eine Größe.
- Sowohl Skalar- als auch Vektorgrößen sind messbar.
- Beide können eine bestimmte physikalische Größe ausdrücken.
- Eine mathematische Operation zwischen Vektor- und Skalargrößen führt zu einer Vektorgröße.
