14 Unterschied zwischen Rekursion und Iteration mit Beispiel

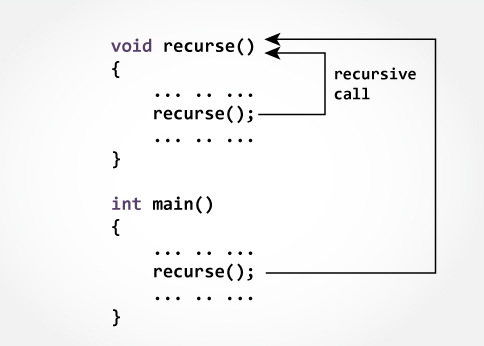
Was ist Rekursion?

Rekursion ist eine Methode zur Lösung eines Problems, bei der die Lösung von Lösungen für kleinere Instanzen desselben Problems abhängt. Der Ansatz kann auf viele Arten von Problemen angewendet werden. Rekursion wird in einer Vielzahl von Disziplinen verwendet, von der Linguistik bis zur Logik. Die häufigste Anwendung der Rekursion findet sich in der Mathematik und Informatik, wo eine definierte Funktion innerhalb ihrer eigenen Definition angewendet wird.

Was ist Iteration?

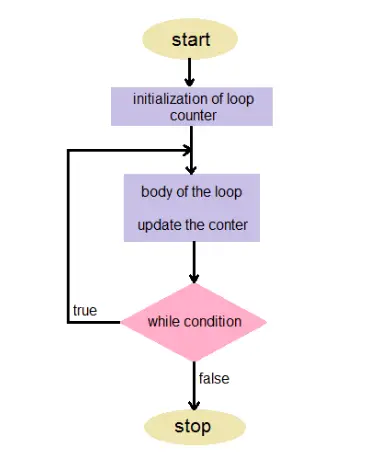
Iteration ist die Wiederholung eines Prozesses, um eine Folge von Ergebnissen zu generieren. Die Sequenz nähert sich einem Endpunkt oder Endwert. Jede Wiederholung des Prozesses ist eine einzelne Iteration und das Ergebnis jeder Iteration ist dann der Ausgangspunkt der nächsten Iteration.

Lesen Sie auch: Unterschied zwischen statischer und dynamischer Speicherzuweisung

Rekursion vs. Iteration in Tabellenform

VERGLEICHSGRUNDLAGE	REKURSION	WIEDERHOLUNG
Beschreibung	Bei der Rekursion handelt es sich um eine rekursive Funktion, die sich selbst wiederholt aufruft, bis eine Basisbedingung nicht erreicht ist (Funktion, die teilweise von ihr selbst definiert ist).	Bei der Iteration werden Schleifen verwendet, durch die eine Menge von Anweisungen wiederholt ausgeführt wird, bis die Bedingung nicht falsch ist (schleifenbasierte Wiederholungen eines Prozesses).
Codegröße	Rekursion hält Ihren Code kurz und einfach.	Der iterative Ansatz macht Ihren Code länger.
Was es beinhaltet	Bei rekursiver Funktion wird nur die Abbruchbedingung (Basisfall) angegeben.	Die Iteration umfasst die Initialisierung, Bedingung und Ausführung der Anweisung innerhalb der Schleife und das Aktualisieren (inkrementieren und dekrementieren) der Steuervariablen.
Gemeinkosten	Rekursive Funktionen bringen einen hohen Overhead mit sich, da jede Funktion den aktuellen Zustand aufruft, Parameter usw. müssen gepusht und aus dem Stack herausgeholt werden.	Bei der Iteration fehlt der Overhead.
Struktur	Rekursion verwendet Auswahlstruktur.	Iteration verwendet Wiederholungsstruktur.
Beendigung	Die Rekursion endet, wenn ein Basisfall erkannt wird.	Die Iteration wird beendet, wenn die Schleifenfortsetzungsbedingung fehlschlägt.
Geschwindigkeit	Aufgrund des Mehraufwands für die Stapelpflege ist die Rekursion relativ langsamer als die Iteration.	Bei der Iteration wird kein Stapel verwendet; Daher ist es relativ schneller als die Rekursion.
Unendliche Bedingung	Eine unendliche Rekursion tritt auf, wenn der Rekursionsschritt das Problem nicht auf eine Weise reduziert, die unter einer bestimmten Bedingung konvergiert (Basisfall).	Eine Endlosschleife tritt bei der Iteration auf, wenn der Schleifenbedingungstest nie falsch wird.
Auswirkung auf die Betriebszeit des Prozessors	Rekursion erhöht die Betriebszeit des Prozessors.	Iteration reduziert die Betriebszeit des Prozessors.
Speichernutzung	Die Rekursion verwendet den Stack-Bereich, um den aktuellen Status der Funktion zu speichern, wodurch die Speicherauslastung relativ hoch ist.	Die Iteration verwendet den permanenten Speicherbereich nur für die Variablen, die an ihrem Codeblock beteiligt sind, und daher ist der Speicherverbrauch relativ gering.
Zeitkomplexität	Sehr hohe (meist exponentielle) Zeitkomplexität.	Relativ geringere Zeitkomplexität (in der Regel polynomial-logarithmisch).
Auswirkung auf die CPU	Unendliche Rekursion kann die CPU zum Absturz bringen.	Bei Endlosschleifen werden CPU-Zyklen wiederholt verwendet.
Anwendung	Fakultät, Fibonacci-Reihe usw.	Mittelwert einer Datenreihe ermitteln, Einmaleins erstellen usw.

Lesen Sie auch : Unterschied zwischen While- und Do-While-Schleife in Java