Trapez- und Simpson-Regel sind beides numerische Verfahren, die zur Annäherung von Werten eines bestimmten Integrals verwendet werden.
Trapezregel
In dieser Regel wird angenommen, dass die Grenzen zwischen den Enden der Ordinaten gerade sind. Daher werden die zwischen der Grundlinie und den unregelmäßigen Grenzlinien eingeschlossenen Flächen als Trapeze bezeichnet.
Was Sie über Trapezregel/Trapezregel wissen müssen
- Das durch die Trapezregel erhaltene Ergebnis wird nicht beeinflusst, da die Grenze zwischen den Ordinaten als gerade betrachtet wird.
- Trapezoidregel kann auch genannt werden Trapezes Regel .
- Trapezregel liefert ein geschätztes Ergebnis. Zum Beispiel ist die durch Trapezregel ermittelte Fläche eines unregelmäßigen Grundstücks nur ein Näherungswert und nicht der genaue Wert.
- Bei der Trapezregel gilt die Grenze zwischen den Ordinaten als gerade.
- Es gibt keine Einschränkung für diese Regel. Diese Regel kann auf eine beliebige Anzahl von Ordinaten angewendet werden.
- Berechnungen, die an der Trapezoidregel beteiligt sind, sind nicht so komplex wie die in der Simpson-Regel.
- Trapezregel kann wie folgt formuliert werden: Zur Summe der ersten und letzten Ordinate wird das Doppelte der Summe der Zwischenordinate addiert. Diese Gesamtsumme wird mit dem gemeinsamen Abstand multipliziert. Die Hälfte dieses Produkts ist die erforderliche Fläche.
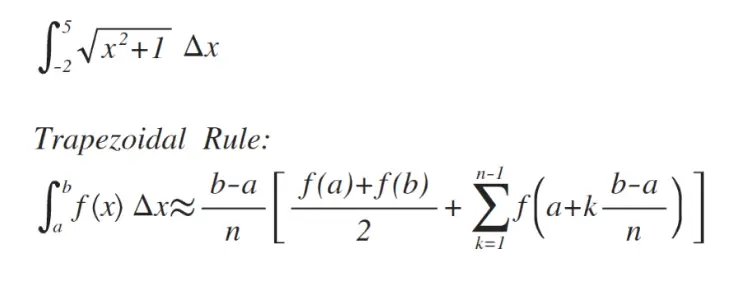
Simpsons Regel
Die Simpson-Regel ist ein numerischer Ansatz, um bestimmte Integrale zu finden, bei denen keine andere Methode möglich ist. Der Wert eines bestimmten Integrals wird durch eine quadratische Funktion angenähert. In dieser Regel wird angenommen, dass die Grenzen zwischen den Enden der Ordinaten einen Parabelbogen bilden. Daher wird die Simpson-Regel manchmal als Parabelregel bezeichnet. Die mit der Simpson-Regel erhaltenen Ergebnisse haben ein hohes Maß an Genauigkeit und werden daher nur verwendet, wenn eine hohe Genauigkeit erforderlich ist.
Simpson-Regel/Parabelregel
- Das durch die Simpson-Regel erhaltene Ergebnis ist größer oder kleiner, da die Kurve der Grenze zur Grundlinie konvex oder konkav ist.
- Die Simpson-Regel kann auch als Parabolische Regel bezeichnet werden .
- Die Simpson-Regel liefert im Vergleich zur Simpson-Regel ein genaues Ergebnis.
- In der Simpson-Regel wird die Grenze zwischen den Ordinaten als ein Bogen einer Parabel betrachtet.
- Diese Regel gilt nur, wenn die Anzahl der Teilungen gerade ist, dh die Anzahl der Ordinaten ungerade ist.
- Es ist ein größerer Rechenaufwand erforderlich und Rundungsfehler können zu einem größeren Problem werden.
- Die Simpson-Regel kann wie folgt formuliert werden: Zur Summe der ersten und der letzten Ordinate wird die vierfache Summe der geraden Ordinaten und die doppelte Summe der verbleibenden ungeraden Ordinaten addiert. Diese Gesamtsumme wird mit dem gemeinsamen Abstand multipliziert. Ein Drittel dieses Produkts ist die erforderliche Fläche.
Unterschied zwischen Trapezregel und Simpson-Regel in Tabellenform
| VERGLEICHSGRUNDLAGE | TRAPEZOIDALE REGEL | SIMPSONS REGEL |
| Ergebnis erhalten | Das durch die Trapezregel erhaltene Ergebnis wird nicht beeinflusst, da die Grenze zwischen den Ordinaten als gerade betrachtet wird. | Das durch die Simpson-Regel erhaltene Ergebnis ist größer oder kleiner, da die Kurve der Grenze zur Grundlinie konvex oder konkav ist. |
| Alternativer Name | Trapezoidregel kann auch genannt werden Trapezes Regel . | Die Simpson-Regel kann auch als Parabolische Regel bezeichnet werden . |
| Genauigkeit | Liefert ein geschätztes Ergebnis. Zum Beispiel ist die durch Trapezregel ermittelte Fläche eines unregelmäßigen Grundstücks nur ein Näherungswert und nicht der genaue Wert. | Liefert ein genaues Ergebnis im Vergleich zur Simpsons-Regel. |
| Grenze zwischen Ordinaten | Die Grenze zwischen den Ordinaten wird als gerade betrachtet. | Die Grenze zwischen den Ordinaten wird als ein Bogen einer Parabel betrachtet. |
| Anwendbarkeit | Es gibt keine Einschränkung für diese Regel. Diese Regel kann auf eine beliebige Anzahl von Ordinaten angewendet werden. | Diese Regel gilt nur, wenn die Anzahl der Teilungen gerade ist, dh die Anzahl der Ordinaten ungerade ist. |
| Berechnung | Berechnungen, die an der Trapezoidregel beteiligt sind, sind nicht so komplex wie die in der Simpson-Regel. | Es ist ein größerer Rechenaufwand erforderlich und Rundungsfehler können zu einem größeren Problem werden. |
| Regel | Zur Summe der ersten und letzten Ordinate wird die doppelte Summe der Zwischenordinate addiert. Diese Gesamtsumme wird mit dem gemeinsamen Abstand multipliziert. Die Hälfte dieses Produkts ist die erforderliche Fläche. | Zur Summe der ersten und letzten Ordinate wird das Vierfache der Summe der geraden Ordinaten und das Doppelte der Summe der verbleibenden ungeraden Ordinaten addiert. Diese Gesamtsumme wird mit dem gemeinsamen Abstand multipliziert. Ein Drittel dieses Produkts ist die erforderliche Fläche. |
| Formel |