Was ist DFS (Depth First Search)?

Tiefere Erste Suche ( DFS ) ist ein Algorithmus zum Verfahren oder die Suche Baum oder Graph Datenstrukturen. Der Algorithmus beginnt am Wurzelknoten (obersten) eines Baums und geht so weit wie möglich einen gegebenen Zweig (Pfad) hinunter, verfolgt dann zurück, bis er einen unerforschten Pfad findet, und untersucht ihn dann. Der Algorithmus tut dies, bis der gesamte Graph untersucht wurde.

Tiefer Erster Search ( DFS ) wird in der Regel als Subroutinen in anderen komplexeren Algorithmen verwendet. Hopcroft-Karp, Tree-Traversal und Matching-Algorithmus sind Beispiele für Algorithmen, die DFS verwenden, um ein Matching in einem Graphen zu finden.

Was ist BFS (Breadth First Search)

Breadth First Search ( BFS ) ist ein Algorithmus zum Durchlaufen oder Durchsuchen von Baum- oder Graphdatenstrukturen. Es beginnt an der Baumwurzel und untersucht alle Nachbarknoten in der aktuellen Tiefe, bevor es zu den Knoten in der nächsten Tiefenebene übergeht.

Breadth First Search (BFS) ist ein wichtiger Suchalgorithmus, der verwendet wird, um viele Probleme zu lösen, einschließlich des Findens des kürzesten Pfads in Graphen und des Lösens von Puzzlespielen (wie Rubik’s Cubes). In der Informatik kann es auch zur Lösung von Graphenproblemen wie der Analyse von Netzwerken, Kartierung von Routen und Scheduling verwendet werden.

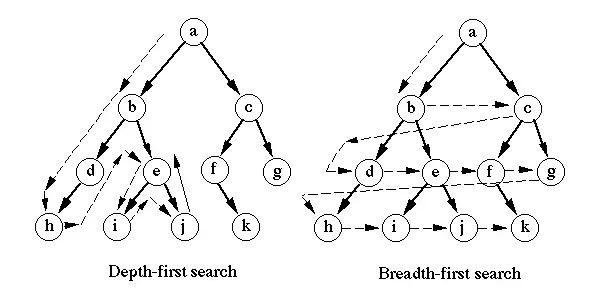
 DFS-Funktionen (Depth First Search)

1. DFS startet die Traversierung vom Wurzelknoten und untersucht die Suche so weit wie möglich vom Wurzelknoten, dh in der Tiefe.
2. Der DFS-Algorithmus arbeitet in zwei Stufen. In der ersten Stufe werden die besuchten Scheitelpunkte auf den Stapel geschoben und später, wenn es keine weiteren Scheitelpunkte mehr gibt, um die herausgezogenen Scheitelpunkte zu besuchen.
3. Die DFS-Suche kann mit Hilfe von Stack-dh LIFO-Implementierungen durchgeführt werden.
4. DFS ist nicht nützlich, um den kürzesten Pfad zu finden. Es wird verwendet, um eine Durchquerung eines allgemeinen Graphen durchzuführen, und die Idee von DFS besteht darin, einen Pfad so lang wie möglich zu machen und dann zurückzugehen (Backtrack), um auch so lange Zweige wie möglich hinzuzufügen.
5. DFS ist im Vergleich zu BFS vergleichsweise schneller.
6. Die Zeitkomplexität von DFS ist O(V+E), wobei V für Ecken und E für Kanten steht.
7. DFS benötigt im Vergleich zu BFS vergleichsweise weniger Speicher.
8. Einige Anwendungen von DFS umfassen: Topologisches Sortieren, Finden verbundener Komponenten, Finden von Artikulationspunkten (Schnittpunkten) des Graphen, Lösen von Rätseln wie Labyrinth und Finden stark verbundener Komponenten.

BFS-Funktionen (Breadth First Search)

1. BFS beginnt die Durchquerung vom Wurzelknoten und untersucht dann die Suche Ebene für Ebene, dh so nah wie möglich am Wurzelknoten.
2. Der BFS-Algorithmus arbeitet in einer einzigen Stufe. Die besuchten Scheitelpunkte werden aus der Warteschlange entfernt und dann sofort angezeigt.
3. BFS kann mit Hilfe einer Warteschlange, dh einer FIFO-Implementierung, durchgeführt werden.
4. BFS ist nützlich, um den kürzesten Weg zu finden. BFS kann verwendet werden, um den kürzesten Abstand zwischen einem Startknoten und den verbleibenden Knoten des Graphen zu finden.
5. BFS ist im Vergleich zu DFS vergleichsweise langsamer.
6. Die Zeitkomplexität von BFS ist O(V+E), wobei V für Ecken und E für Kanten steht.
7. BFS benötigt im Vergleich zu DFS vergleichsweise mehr Speicher.
8. Einige Anwendungen von BFS umfassen: Finden verbundener Komponenten in einem Graphen, Testen eines Graphen auf Bipartitität, Finden aller Knoten innerhalb einer verbundenen Komponente und Finden des kürzesten Pfads zwischen zwei Knoten.

Unterschied zwischen DFS und BFS in Tabellenform

VERGLEICHSGRUNDLAGE	DFS	BFS
	Es startet die Durchquerung vom Wurzelknoten und untersucht die Suche so weit wie möglich vom Wurzelknoten, dh in der Tiefe.	BFS beginnt die Durchquerung vom Wurzelknoten und untersucht dann die Suche Ebene für Ebene, dh so nah wie möglich am Wurzelknoten.
Arbeitsschritte des Algorithmus	Der Algorithmus arbeitet in zwei Stufen. In der ersten Stufe werden die besuchten Scheitelpunkte auf den Stapel geschoben und später, wenn es keine weiteren Scheitelpunkte mehr gibt, um die herausgezogenen Scheitelpunkte zu besuchen.	Der Algorithmus arbeitet in einer einzigen Stufe. Die besuchten Scheitelpunkte werden aus der Warteschlange entfernt und dann sofort angezeigt.
Suche	Seine Suche kann mit Hilfe von Stack-dh LIFO-Implementierungen durchgeführt werden.	Seine Suche kann mit Hilfe einer Warteschlange, dh einer FIFO-Implementierung, durchgeführt werden.
Nützlichkeit	Es ist nicht nützlich, den kürzesten Weg zu finden. Es wird verwendet, um eine Durchquerung eines allgemeinen Graphen durchzuführen, und die Idee von DFS besteht darin, einen Pfad so lang wie möglich zu machen und dann zurückzugehen (Backtrack), um auch so lange Zweige wie möglich hinzuzufügen.	Es ist nützlich, den kürzesten Weg zu finden. BFS kann verwendet werden, um den kürzesten Abstand zwischen einem Startknoten und den verbleibenden Knoten des Graphen zu finden.
Geschwindigkeit	Es ist im Vergleich zu BFS vergleichsweise schneller.	Im Vergleich zu DFS ist es vergleichsweise langsamer.
Zeitkomplexität	Die Zeitkomplexität von BFS ist O(V+E), wobei V für Ecken und E für Kanten steht.	Die Zeitkomplexität von BFS ist O(V+E), wobei V für Ecken und E für Kanten steht.
Speicherbedarf	DFS benötigt im Vergleich zu BFS vergleichsweise weniger Speicher.	Es erfordert vergleichsweise mehr Speicher zu DFS.
Anwendung	Topologische Sortierung Finden verbundener Komponenten Finden von Artikulationspunkten (Schnittpunkten) des Graphen. Lösen von Rätseln wie Labyrinth. Suche nach stark verbundenen Komponenten.	Suchen verbundener Komponenten in einem Graphen Testen eines Graphen auf Bipartitität Finden aller Knoten innerhalb einer verbundenen Komponente. Den kürzesten Weg zwischen zwei Knoten finden