Was ist das NP-Problem?
Dies sind die Entscheidungsprobleme, die in polynomieller Zeit verifiziert werden können. Das heißt, wenn ich behaupte, dass es für ein bestimmtes Problem eine polynomiale Zeitlösung gibt, bitten Sie mich, dies zu beweisen. Dann gebe ich Ihnen einen Beweis, den Sie in polynomieller Zeit leicht verifizieren können. Diese Art von Problemen nennt man NP-Probleme. Beachten Sie, dass wir hier nicht darüber sprechen, ob es für dieses Problem eine polynomielle Zeitlösung gibt oder nicht. Aber wir sprechen davon, die Lösung eines gegebenen Problems in polynomieller Zeit zu verifizieren.
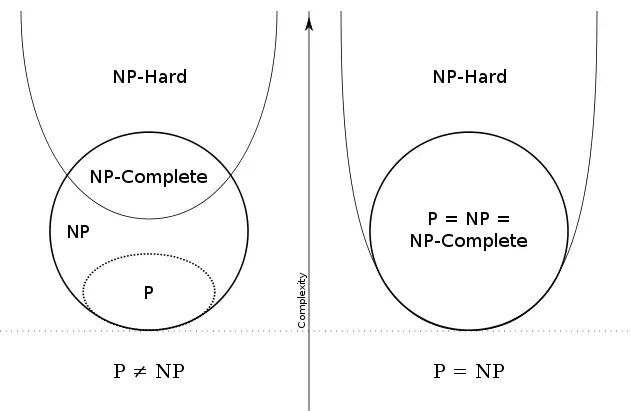
Um den Rest der Frage zu beantworten, müssen Sie zunächst verstehen, welche NP-schweren Probleme auch NP-vollständig sind. Wenn ein NP-schweres Problem zur Menge NP gehört, dann ist es NP-vollständig. Um zur Menge NP zu gehören, muss ein Problem
(i) Ein Entscheidungsproblem,
(ii) Die Anzahl der Lösungen für das Problem sollte endlich sein und jede Lösung von Polynomlänge sein sollte, und
(iii) Bei einer Polynomlänge Lösung, sollten wir in der Lage sein zu sagen , ob die Antwort auf dem Problem ist ja/nein.
Was ist das NP-vollständige Problem?
Dies sind die Probleme, die sowohl NP als auch NP-schwer sind. Das heißt, wenn wir diese Probleme lösen können, können wir jedes andere NP-Problem lösen und die Lösungen dieser Probleme können in polynomieller Zeit verifiziert werden.
Mit anderen Worten, NP-vollständig ist eine Komplexitätsklasse, die die Menge aller Probleme X in NP darstellt, für die es möglich ist, jedes andere NP-Problem Y auf X polynomiale Zeit zu reduzieren .
Intuitiv bedeutet dies, dass wir Y schnell lösen können, wenn wir wissen, wie man X schnell löst . Genau, Y ist reduzierbar auf X, wenn es einen Polynomialzeitalgorithmus gibt, f um Instanzen y von Y in Instanzen x = f(y) von X in polynomieller Zeit zu transformieren , mit der Eigenschaft, dass die Antwort auf y ja ist, genau dann, wenn die Antwort auf f(y) ja ist.
Beispiel
3-SAT. Dies ist das Problem, bei dem wir eine Konjunktion (UNDs) von 3-Klausel-Disjunktionen (ORs) erhalten, Aussagen der Form
(x_v11 OR x_v21 OR x_v31) AND
(x_v12 OR x_v22 OR x_v32) AND
... AND
(x_v1n OR x_v2n OR x_v3n)
wobei jede x_vij eine boolesche Variable oder die Negation einer Variablen aus einer endlichen vordefinierten Liste ist (x_1, x_2, ... x_n).
Es kann gezeigt werden, dass jedes NP-Problem auf 3-SAT reduziert werden kann . Der Beweis dafür ist technisch und erfordert die Verwendung der technischen Definition von NP ( basierend auf nichtdeterministischen Turingmaschinen ). Dies ist als Theorem von Cook bekannt .
Was NP-vollständige Probleme so wichtig macht, ist, dass jedes NP-Problem in polynomieller Zeit lösbar ist (ein Problem, um alle zu beherrschen).
Was Sie über NP Complete wissen müssen
- NP-vollständige Probleme können durch deterministische Algorithmen in polynomieller Zeit gelöst werden.
- Um dieses Problem zu lösen, muss es sowohl ein NP- als auch ein NP-schweres Problem sein.
- Es ist ausschließlich ein Entscheidungsproblem.
- Beispiele sind: Minesweeper-Problem, Bestimmen, ob ein Graph einen Hamilton-Zyklus hat, Bestimmen, ob eine Boolesche Formel erfüllbar ist oder nicht usw.
Was ist ein NP-schweres Problem?
Diese sind mindestens so schwer wie die schwierigsten Probleme in NP. Wenn wir diese Probleme in polynomieller Zeit lösen können, können wir jedes mögliche NP-Problem lösen. Beachten Sie, dass diese Probleme nicht unbedingt NP-Probleme sind. Das heißt, wir können die Lösung dieser Probleme in polynomieller Zeit verifizieren.
Intuitiv sind dies die Probleme, die mindestens so schwer sind wie die NP-vollständigen Probleme . Beachten Sie, dass NP-schwere Probleme müssen nicht in NP sein , und sie müssen nicht Entscheidungsprobleme sein .
Die genaue Definition hier ist, dass ein Problem X NP-schwer ist, wenn es ein NP-vollständiges Problem gibt Y, das Y auf X in polynomieller Zeit reduzierbar ist .
Da aber jedes NP-vollständige Problem in polynomieller Zeit auf jedes andere NP-vollständige Problem reduziert werden kann, können alle NP-vollständigen Probleme in polynomieller Zeit auf jedes NP-schwere Problem reduziert werden. Wenn es dann eine Lösung für ein NP-schweres Problem in polynomialer Zeit gibt, gibt es eine Lösung für alle NP-Probleme in polynomialer Zeit.
Beispiel
Das Halteproblem ist ein NP-schweres Problem. Dies ist das Problem, bei dem ein Programm P und eine Eingabe Iangehalten werden. Dies ist ein Entscheidungsproblem, aber es ist nicht in NP. Es ist klar, dass jedes NP-vollständige Problem auf dieses reduziert werden kann. Als weiteres Beispiel ist jedes NP-vollständige Problem NP-schwer.
Was Sie über das schwierige NP-Problem wissen müssen
- NP-schwere Probleme (zB X) können genau dann gelöst werden, wenn ein NP-vollständiges Problem (zB Y) in polynomieller Zeit auf X reduzierbar ist.
- Um dieses Problem zu lösen, muss es ein NP-Problem sein.
- Es ist kein Entscheidungsproblem.
- Beispiele sind: Halteproblem, Vertex-Cover-Problem, Circuit-Erfüllbarkeitsproblem usw.
Lesen Sie auch: Unterschied zwischen P- und NP-Problemen
Unterschied zwischen NP-hartem und NP-vollständigem Problem in Tabellenform
| VERGLEICHSGRUNDLAGE | NP HARTES PROBLEM | NP KOMPLETTES PROBLEM |
| Beschreibung | NP-schwere Probleme (zB X) können genau dann gelöst werden, wenn ein NP-vollständiges Problem (zB Y) in polynomieller Zeit auf X reduzierbar ist. | NP-vollständige Probleme können durch deterministische Algorithmen in polynomieller Zeit gelöst werden. |
| Lösung | Um dieses Problem zu lösen, muss es ein NP-Problem sein. | Um dieses Problem zu lösen, muss es sowohl ein NP- als auch ein NP-schweres Problem sein. |
| Art des Problems | Es ist kein Entscheidungsproblem. | Es ist ausschließlich ein Entscheidungsproblem. |
| Beispiele | -Halting-Problem -Vertex-Cover-Problem -Circuit-Erfüllbarkeitsproblem usw. | -Minesweeper-Problem -Bestimmen, ob ein Graph einen Hamilton-Zyklus hat. -Bestimmen, ob die Boolesche Formel erfüllbar ist oder nicht |