14 Unterschied zwischen Baum und Diagramm |(Baum vs. Diagramm)

In der Programmierung können Daten in Datenstrukturen wie Graphen und Bäumen gespeichert werden. Ein Baum ist typischerweise eine Sonderform eines Graphen, dh ein minimal zusammenhängender Graph und hat nur einen Pfad zwischen zwei beliebigen Knoten. Mit anderen Worten ist der Baum ein Sonderfall eines Graphen ohne Schleifen, Schaltkreise und keine Selbst-Schleifen. Graphen können Schleifen, Schaltungen sowie Selbstschleifen haben.  

Bäume

Baum in Datenstrukturen ist eine hierarchische Datenstruktur, die Informationen natürlich in Form eines Hierarchiestils speichert. Bäume werden verwendet, um Datenstrukturen zu definieren und als Grundlage für Algorithmen zur Lösung von Problemen. Im Vergleich zu Arrays, verknüpften Listen, Stapeln und Warteschlangen, die lineare Datenstrukturen sind, ist ein Baum eine nichtlineare Datenstruktur.

Genau wie ein Graph ist eine Baumdatenstruktur eine Sammlung von Knoten. Die Knoten können dann Kinderknoten haben. Die Kinderknoten können ihre eigenen Kinderknoten haben, die als Enkelknoten bezeichnet werden. Das HTML-DOM verwendet beispielsweise eine Baumdatenstruktur, um die Hierarchie der Elemente darzustellen.

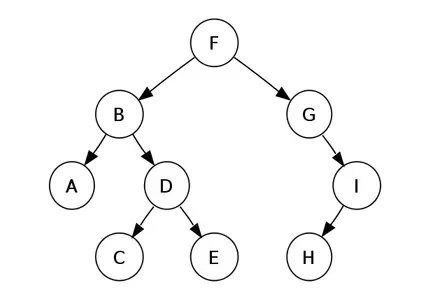
Begriffe im Zusammenhang mit Bäumen

• Root Node : Dies ist der oberste Knoten des Baums.
• Child : Dies ist der Knoten, der durch übergeordnete Knoten verbunden ist.
• Kante: Kanten werden verwendet, um zwei Knoten zu verbinden.
• Geordneten Knoten : Der Wurzelknoten in der Struktur, die eine oder mehr als einen Referenzknoten oder zeigt auf andere Knoten.
• Blattknoten: Dies ist der Knoten, der kein Kind in der Struktur hat.
• Level: Ein Level kann als die Höhe eines Baumes angesehen werden. Im Baum steigt die Höhe von oben nach unten, wobei der Wurzelknoten auf der Ebene 0 lag und der Blattknoten am unteren Ende eines Baums oder Unterbaums lag.

Was Sie über Bäume wissen müssen (Eigenschaften)

1. Baum ist eine Sonderform des Graphen, dh ein minimal zusammenhängender Graph, der nur einen Pfad zwischen zwei beliebigen Knoten hat.
2. Baumdatenstrukturen sind hierarchische, nichtlineare Sammlungen von verknüpften Knoten.
3. In Bäumen gibt es viele Regeln/Einschränkungen, um Verbindungen zwischen Knoten durch Kanten herzustellen.
4. Verschiedene Arten von Bäumen, die auf verschiedenen Eigenschaften basieren, umfassen Binärbaum, Binärsuchbaum, AVL-Baum, Heaps usw.
5. Vorbestellung, Nachbestellung und Nachbestellung sind eine Art von Logarithmen, die in Bäumen verwendet werden, um alle Elemente zu durchlaufen.
6. Ein Beispiel für einen Baum ist das HTML-DOM, bei dem jedes andere Tag hierarchisch aus dem html-Doctype-Tag fließt.
7. Ein Baum kann keine Schleifenstruktur haben.
8. Bäume können als DAG (Directed Acyclic Graphs) kategorisiert werden. DAG ist eine Art gerichteter Graph, der keine Zyklen hat.
9. In Bäumen gibt es eine Eltern-Kind-Beziehung, jedes Kind kann nur einen Elternteil haben und daher kann der Fluss von oben nach unten oder umgekehrt erfolgen.
10. In Bäumen gibt es genau einen Wurzelknoten und jedes Kind hat nur einen Elternteil.
11. Wenn Bäume „n“ Ecken haben, dann dürfen sie nur genau „n-1“ Kanten haben.
12. Bäume sind im Vergleich zu Graphen weniger komplex, da sie keine Zyklen und Selbstschleifen haben, aber dennoch verbunden sind.
13. Tree ist ein Sonderfall von Graphen ohne Schleifen, ohne Schaltungen und Selbstschleifen.
14. Wird beim Sortieren, Suchen, Durchlaufen und bei der binären Suche verwendet.

Graph

Graphen in der JavaScript-Programmierung sind eine Datenstruktur, die aus einer Sammlung von Knoten mit Kanten besteht. Eine Kante ist ein Paar von Knoten, die verbunden sind. Sie werden hauptsächlich verwendet, um ein Modell zu beschreiben, das die Route von einem Ort zu einem anderen Ort zeigt. Ein Graph kann gerichtet oder ungerichtet sein.

Ein gerichteter Graph enthält Kanten, die ähnlich wie eine Einbahnstraße funktionieren. Die Kanten fließen von einem Knoten zum anderen . Zum Beispiel können Sie eine grafische Darstellung von Menschen und Autos oder Fernseher haben , wo jede Person mehrere Lieblingsautos oder Fernseher aber Autos oder Fernseher haben keinen Lieblings Person haben kann.

Ein ungerichteter Graph hat Kanten, die bidirektional verlaufen, ähnlich einer zweispurigen Straße mit Verkehr in beide Richtungen.  Zum Beispiel können Sie eine grafische Darstellung von Ziegen haben , wobei jede Ziege einen Eigentümer hat und jeder Besitzer eine Ziege hat.

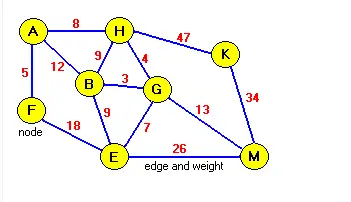
Mit Graphen verbundene Begriffe

• Zyklus : Dies ist ein Pfad, bei dem der erste und der letzte Scheitelpunkt gleich sind.
• Pfad : Ein Pfad von einem zufälligen Knoten w ist eine benachbarte Folge von Knoten.
• Vertices: Vertices sind die auf dem Graphen vorhandenen Knoten, die mit Hilfe von Kanten verbunden sind.
• Grad:   Dies ist die Anzahl der Kanten, die auf einen Scheitelpunkt fallen.
• Verbundener Graph: Falls es einen Pfad von einem zufälligen Knoten zu einem anderen Knoten gibt, dann kann der Graph als verbundener Graph beschrieben werden.

Was Sie über Graphen wissen müssen (Eigenschaften)

1. In einem Graphen kann es mehr als einen Pfad geben, dh ein Graph kann einen unidirektionalen oder bidirektionalen Pfad (Kanten) zwischen den Knoten haben.
2. Graphen-Datenstrukturen sind Sammlungen verknüpfter Knoten in nichtlinearen Netzwerkmodellen.
3. In Graphen gibt es keine Einschränkungen/Regeln für die Verbindung der Knoten durch Kanten.
4. Es gibt nur zwei Arten von Graphen, die auf unterschiedlichen Eigenschaften basieren, nämlich gerichtete und ungerichtete Graphen.
5. Breath First Search, Depth First Search sind eine Art Suchalgorithmus in Graphen, um jedes Element zu durchsuchen.
6. Ein gutes Beispiel für ein Netzwerkdiagramm ist eine Straßenkarte innerhalb einer Stadt.
7. Ein Graph kann eine Schleifenstruktur haben, was bedeutet, dass das letzte Element und das erste Element gleich sind.
8. Der Graph kann zyklisch oder azyklisch sein.
9. In Diagrammen gibt es keine Eltern-Kind-Beziehung.
10. Es gibt kein Konzept des Wurzelknotens in Graphen.
11. In Graphen hängt die Anzahl der Kanten nicht von der Anzahl der Knoten ab.
12. Graphen sind im Vergleich zu Bäumen komplexer, da sie Zyklen und Schleifen haben.
13. Graph kann Schleifen, Schaltungen sowie Selbstschleifen haben.
14. Einige Anwendungen von Graphen umfassen das Einfärben von Karten, die Jobplanung, die in Algorithmen der Datenwissenschaft und des maschinellen Lernens verwendet werden.

Lesen Sie auch: Unterschied zwischen binärem Baum und binärem Suchbaum

Unterschied zwischen Baum und Diagramm in Tabellenform

VERGLEICHSGRUNDLAGE	BAUM	GRAPH
Beschreibung	Baum ist eine Sonderform des Graphen, dh ein minimal zusammenhängender Graph, der nur einen Pfad zwischen zwei beliebigen Knoten hat.	In einem Graphen kann es mehr als einen Pfad geben, dh ein Graph kann einen unidirektionalen oder bidirektionalen Pfad (Kanten) zwischen den Knoten haben.
Struktur	Baumdatenstrukturen sind hierarchische, nichtlineare Sammlungen von verknüpften Knoten.	Graphen-Datenstrukturen sind Sammlungen verknüpfter Knoten in nichtlinearen Netzwerkmodellen.
Regeln/Einschränkungen	In Bäumen gibt es viele Regeln/Einschränkungen, um Verbindungen zwischen Knoten durch Kanten herzustellen.	In Graphen gibt es keine Einschränkungen/Regeln für die Verbindung der Knoten durch Kanten.
Typen	Binärbaum, binärer Suchbaum, AVL-Baum, Heaps etc.	Gerichtete und ungerichtete Graphen.
Suchalgorithmus	Vorbestellung, Nachbestellung und Nachbestellung sind eine Art von Logarithmen, die in Bäumen verwendet werden, um alle Elemente zu durchlaufen.	Breath First Search, Depth First Search sind eine Art Suchalgorithmus in Graphen, um jedes Element zu durchsuchen.
Beispiel	Ein Beispiel für einen Baum ist das HTML-DOM, bei dem jedes andere Tag hierarchisch aus dem html-Doctype-Tag fließt.	Ein gutes Beispiel für ein Netzwerkdiagramm ist eine Straßenkarte innerhalb einer Stadt.
Schleifenstruktur	Ein Baum kann keine Schleifenstruktur haben.	Ein Graph kann eine Schleifenstruktur haben, was bedeutet, dass das letzte Element und das erste Element gleich sind.
Kategorien	Bäume können als DAG (Directed Acyclic Graphs) kategorisiert werden. DAG ist eine Art gerichteter Graph, der keine Zyklen hat.	Der Graph kann zyklisch oder azyklisch sein.
Eltern-Kind-Beziehung	In Bäumen gibt es eine Eltern-Kind-Beziehung, jedes Kind kann nur einen Elternteil haben und daher kann der Fluss von oben nach unten oder umgekehrt erfolgen.	In Diagrammen gibt es keine Eltern-Kind-Beziehung.
Konzept des Wurzelknotens	In Bäumen gibt es genau einen Wurzelknoten und jedes Kind hat nur einen Elternteil.	Es gibt kein Konzept des Wurzelknotens in Graphen.
Kanten und Scheitelpunkte	Wenn Bäume „n“ Ecken haben, dann dürfen sie nur genau „n-1“ Kanten haben.	In Graphen hängt die Anzahl der Kanten nicht von der Anzahl der Knoten ab.
Komplexität	Bäume sind im Vergleich zu Graphen weniger komplex, da sie keine Zyklen und Selbstschleifen haben, aber dennoch verbunden sind.	Graphen sind im Vergleich zu Bäumen komplexer, da sie Zyklen und Schleifen haben.
Komponenten	Tree ist ein Sonderfall von Graphen ohne Schleifen, ohne Schaltungen und Selbstschleifen.	Graph kann Schleifen, Schaltungen sowie Selbstschleifen haben.
Anwendung	Wird beim Sortieren, Suchen, Durchlaufen und bei der binären Suche verwendet.	Einige Anwendungen von Graphen umfassen das Einfärben von Karten, die Jobplanung, die in Algorithmen der Datenwissenschaft und des maschinellen Lernens verwendet werden.