Lineare und logistische Regression sind zwei gängige Techniken der Regressionsanalyse, die zur Analyse eines Datensatzes im Finanz- und Investitionsbereich verwendet werden und Managern helfen, fundierte Entscheidungen zu treffen. Lineare und logistische Regressionen sind einer der einfachsten maschinellen Lernalgorithmen, die unter die Technik des überwachten Lernens fallen und zur Klassifizierung und Lösung von Regressionsproblemen verwendet werden. Es gibt zwei wichtige Variablen bei der Regression; sie umfassen abhängige und unabhängige Variable. Die abhängige Variable ist die Hauptvariable, die Sie verstehen möchten , während die unabhängige Variable Faktoren umfasst, die einen signifikanten Einfluss auf die abhängige Variable haben können.
Was ist lineare Regression?
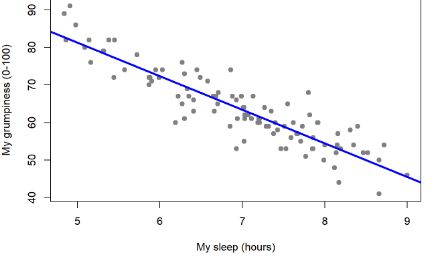
Die lineare Regression ist eine Technik der Regressionsanalyse, die die Beziehung zwischen zwei Variablen mithilfe einer geraden Linie herstellt. Die lineare Regression versucht, eine gerade Linie zu zeichnen, die den Daten am nächsten kommt, indem die Steigung und der Schnittpunkt ermittelt werden, die die Linie definieren, und Regressionsfehler minimiert werden. Wenn eine einzelne unabhängige Variable zur Schätzung des Outputs verwendet wird, wird die Analyse als einfache lineare Regression bezeichnet, während mehr als zwei unabhängige Variablen zur Schätzung des Outputs verwendet werden, wird eine solche Regressionsanalyse als multiple lineare Regression bezeichnet.
Multiple Regression ist eine breitere Klasse von Regressionen, die lineare und nichtlineare Regressionen mit mehreren erklärenden Variablen umfasst. Multiple Regressionen basieren auf der Annahme, dass sowohl zwischen den abhängigen als auch den unabhängigen Variablen eine lineare Beziehung besteht. Es wird auch keine größere Korrelation zwischen den unabhängigen Variablen angenommen.
Die lineare Regression ist einer der einfachsten maschinellen Lernalgorithmen, der unter die Technik des überwachten Lernens fällt und zur Lösung von Regressionsproblemen verwendet wird. Es wird verwendet, um die kontinuierliche abhängige Variable mit Hilfe unabhängiger Variablen zu schätzen. Dies geschieht durch das Finden der besten Anpassungslinie, die das Ergebnis für die kontinuierliche abhängige Variable genau vorhersagt.
Die Anwendung der linearen Regression basiert auf der Methode der kleinsten Quadrate, die besagt, dass die Regressionskoeffizienten so gewählt werden müssen, dass die Summe der quadrierten Distanzen jeder beobachteten Reaktion auf ihren angepassten Wert minimiert wird. Aufgrund der Verwendung einer geraden Linie, um die Eingabevariablen den abhängigen Variablen zuzuordnen, ist die Ausgabe für die lineare Regression ein kontinuierlicher Wert wie Alter, Preis, Gehalt usw.; und somit kann die Ausgabe eine unendliche Zahl sein. Dies bedeutet, dass die Ausgaben positiv oder negativ sein können, ohne maximale oder minimale Grenzen.
Was Sie über die lineare Regression wissen müssen
- Der Zweck der linearen Regression besteht darin, die kontinuierliche abhängige Variable im Falle einer Änderung der unabhängigen Variablen zu schätzen. Zum Beispiel das Verhältnis zwischen geleisteten Arbeitsstunden und Ihrem Lohn.
- Die lineare Regression nimmt eine normale oder Gaußsche Verteilung der abhängigen Variablen an. Gaussian ist dasselbe wie die Normalverteilung.
- Die lineare Regression erfordert, dass der Fehlerterm normal verteilt wird.
- Die Ausgabe für die lineare Regression muss ein kontinuierlicher Wert wie Alter, Preis, Gewicht usw. sein.
- Bei der linearen Regression muss die Beziehung zwischen abhängiger Variable und unabhängiger Variable linear sein.
- Bei der linearen Regression geht es darum, eine gerade Linie in die Daten einzupassen. Diesbezüglich erfolgt dies durch Auffinden der besten Anpassungslinie (Anpassungsgerade), auch als Regressionslinie bezeichnet, die dann verwendet wird, um die Ausgabe zu schätzen.
- Bei der linearen Regression wird davon ausgegangen, dass alle Residuen für alle vorhergesagten abhängigen Variablenwerte ungefähr gleich sind.
- Die Interpretation von Betas oder Koeffizienten der linearen Regression ist einfach und unkompliziert.
- Lineare Regression wird zur Lösung von Regressionsproblemen beim maschinellen Lernen verwendet.
- Die Anwendung der linearen Regression basiert auf der Methode der kleinsten Quadrate, die besagt, dass die Regressionskoeffizienten so gewählt werden müssen, dass die Summe der quadrierten Distanzen jeder beobachteten Reaktion auf ihren angepassten Wert minimiert wird.
- Bei der Analyse der Stichprobe erfordert die lineare Regression mindestens 5 Ereignisse pro unabhängiger Variable.
- Die lineare Regression ist ein einfacher Prozess und benötigt im Vergleich zur logistischen Regression relativ weniger Rechenzeit.
Was ist logistische Regression?
Die logistische Regression ist eine Technik der Regressionsanalyse zum Analysieren eines Datensatzes, in dem es eine oder mehrere unabhängige Variablen gibt, die ein Ergebnis bestimmen. Es ist einer der beliebtesten maschinellen Lernalgorithmen, die unter überwachte Lerntechniken fallen. Es kann sowohl für Klassifikations- als auch für Regressionsprobleme verwendet werden.
Die logistische Regression liefert eine Ausgabe zwischen 0 und 1, die versucht, die Wahrscheinlichkeit des Eintretens eines Ereignisses zu erklären. Wenn die Ausgabe unter 0,5 liegt, bedeutet dies, dass das Ereignis wahrscheinlich nicht eintritt, während bei einer Ausgabe über 0,5 das Auftreten des Ereignisses wahrscheinlich ist. Im Wesentlichen schätzt die logistische Regression die Wahrscheinlichkeit eines binären Ergebnisses, anstatt das Ergebnis selbst vorherzusagen. Die logistische Regression wird auch in Fällen verwendet, in denen eine lineare Beziehung zwischen dem Output und den Faktoren besteht. In diesem Fall liefert die logistische Regression eine Antwort vom Typ JA oder NEIN .
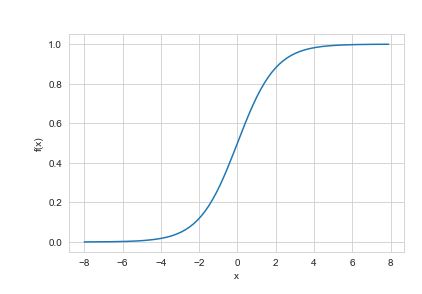
Die Anwendung der logistischen Regression basiert auf der Maximum Likelihood Estimation Method, die besagt, dass Koeffizienten so gewählt werden müssen, dass sie die Wahrscheinlichkeit von Y zu X (Likelihood) maximieren. Es ist auch wichtig zu beachten, dass wir bei der logistischen Regression die gewichtete Summe der Eingaben durch eine Aktivierungsfunktion leiten, die Werte zwischen 0 und 1 abbilden kann. Die Aktivierungsfunktion wird allgemein als Sigmoid-Funktion bezeichnet und die erhaltene Kurve wird als Sigmoid . bezeichnet Kurve oder einfach S-Kurve.
Was Sie über logistische Regression wissen müssen
- Der Zweck der logistischen Regression besteht darin, die kategoriale abhängige Variable unter Verwendung eines gegebenen Satzes unabhängiger Variablen zu schätzen. Beispielsweise kann die logistische Regression verwendet werden, um die Wahrscheinlichkeit eines Ereignisses zu berechnen. Ein Ereignis kann beispielsweise sein, ob das Unternehmen in den nächsten 12 Monaten noch bestehen wird oder nicht.
- Die logistische Regression geht von einer Binomialverteilung der abhängigen Variablen aus.
- Die logistische Regression erfordert keine normale Verteilung des Fehlerterms.
- Der Ausgabewert der logistischen Regression muss ein kategorialer Wert wie 0 oder 1, Ja oder Nein sein.
- Bei der logistischen Regression muss die Beziehung zwischen abhängiger Variable und unabhängiger Variable nicht unbedingt linear sein.
- Bei der logistischen Regression geht es darum, eine Kurve an die Daten anzupassen. In dieser Hinsicht verwendet sie eine S-förmige Kurve, um die Stichproben zu klassifizieren. Positive Steigungen führen zu einer S-förmigen Kurve und negative Steigungen führen zu einer Z-förmigen Kurve.
- Bei der logistischen Regression müssen die Residuen nicht unbedingt für jede Ebene der vorhergesagten abhängigen Variablenwerte gleich sein.
- Bei der logistischen Regression hängt die Koeffizienteninterpretation von log, invers-log, binomial usw. ab, daher ist sie irgendwie komplex.
- Die logistische Regression wird zur Lösung von Klassifikationsproblemen beim maschinellen Lernen verwendet.
- Die Anwendung der logistischen Regression basiert auf der Maximum Likelihood Estimation Method, die besagt, dass Koeffizienten so gewählt werden müssen, dass sie die Wahrscheinlichkeit von Y zu X (Likelihood) maximieren.
- Bei der Analyse der Stichprobe erfordert die logistische Regression mindestens 10 Ereignisse pro unabhängiger Variable.
- Die logistische Regression ist ein iterativer Prozess mit maximaler Wahrscheinlichkeit und erfordert dort im Vergleich zur linearen Regression eine relativ längere Rechenzeit.
Unterschied zwischen linearer Regression und logistischer Regression in Tabellenform
| VERGLEICHSGRUNDLAGE | LINEARE REGRESSION | LOGISTISCHE REGRESSION |
| Zweck | Der Zweck der linearen Regression besteht darin, die kontinuierliche abhängige Variable im Falle einer Änderung der unabhängigen Variablen zu schätzen. | Der Zweck der logistischen Regression besteht darin, die kategoriale abhängige Variable unter Verwendung eines gegebenen Satzes unabhängiger Variablen zu schätzen. |
| Verteilung | Es wird von einer Normal- oder Gaußschen Verteilung der abhängigen Variablen ausgegangen. | Es wird eine Binomialverteilung der abhängigen Variablen angenommen. |
| Fehler Begriff | Es erfordert, dass der Fehlerterm normal verteilt wird. | Es erfordert keine normale Verteilung des Fehlerterms. |
| Ausgabewert | Die Ausgabe für die lineare Regression muss ein kontinuierlicher Wert wie Alter, Preis, Gewicht usw. sein. | Der Ausgabewert der logistischen Regression muss ein kategorialer Wert wie 0 oder 1, Ja oder Nein sein. |
| Beziehung zwischen abhängiger und unabhängiger Variable | Der Zusammenhang zwischen abhängiger Variable und unabhängiger Variable muss linear sein. | Die Beziehung zwischen abhängiger Variable und unabhängiger Variable muss nicht unbedingt linear sein. |
| Ziel | Bei der linearen Regression geht es darum, eine gerade Linie in die Daten einzupassen. Diesbezüglich erfolgt dies durch Auffinden der besten Anpassungslinie (Anpassungsgerade), auch als Regressionslinie bezeichnet, die dann verwendet wird, um die Ausgabe zu schätzen. | Bei der logistischen Regression geht es darum, eine Kurve an die Daten anzupassen. In dieser Hinsicht verwendet sie eine S-förmige Kurve, um die Stichproben zu klassifizieren. |
| Rückstände | Es wird davon ausgegangen, dass alle Residuen für alle vorhergesagten abhängigen Variablenwerte ungefähr gleich sind. | Residuen müssen nicht unbedingt für jede Ebene der vorhergesagten abhängigen Variablenwerte gleich sein. |
| Koeffizienteninterpretation | Die Interpretation von Betas oder Koeffizienten der linearen Regression ist einfach und unkompliziert. | Der Koeffizient der logistischen Regressionsinterpretation hängt von Log, Invers-Log, Binomial usw. ab und ist daher irgendwie komplex. |
| Anwendung | Es wird zur Lösung von Regressionsproblemen beim maschinellen Lernen verwendet. | Es wird zur Lösung von Klassifizierungsproblemen beim maschinellen Lernen verwendet. |
| Grundlage der Anwendung | Die Anwendung der linearen Regression basiert auf der Methode der kleinsten Quadrate | Die Anwendung der logistischen Regression basiert auf der Maximum Likelihood Estimation Method |
| Analyse der Probe | Bei der Probenanalyse sind mindestens 5 Ereignisse pro unabhängiger Variable erforderlich. | Bei der Probenanalyse sind mindestens 10 Ereignisse pro unabhängiger Variable erforderlich. |
| Rechenzeit | Es ist ein einfacher Prozess, dessen Berechnung im Vergleich zur logistischen Regression relativ wenig Zeit in Anspruch nimmt. | Es handelt sich um einen iterativen Prozess mit maximaler Wahrscheinlichkeit und erfordert im Vergleich zur linearen Regression eine relativ längere Rechenzeit. |